Controlling thermal movement in metal panel roofs

By Maciek Rupar
The term ‘thermal movement’ refers to a material’s dimensional changes resulting from temperature swings. A material experiencing a rise or decrease of temperature expands or contracts, respectively—this poses an interesting challenge when it comes to designing metal panel roof assemblies.
The net change in any one dimension is proportional to the net temperature change; this material-specific property is called the co-efficient of linear expansion (CLE). Figure 1 shows CLEs for metals commonly used in roofing.
Thermal movement may produce stresses in metal panel roof assemblies for several reasons. Some of these include:
- materials with different CLEs pushing or pulling against each other at connection points;
- Some components are exposed to a greater shift in temperature than others (e.g. exterior panels experience greater temperature range than the interior structure to which they are attached); and
- movement of components occurring in different directions (e.g. panel lengths must accommodate ridge-to-eave movement, while ridge flashing must accommodate horizontal movement).
The 2016 NRCA Roofing Manual: Metal Panel and SPF Roof Systems provides the National Roofing Contractors Association’s best-practice recommendations for designers of metal panel roof assemblies. This article is based on the treatment of metal panel roof system thermal movement found in the manual.
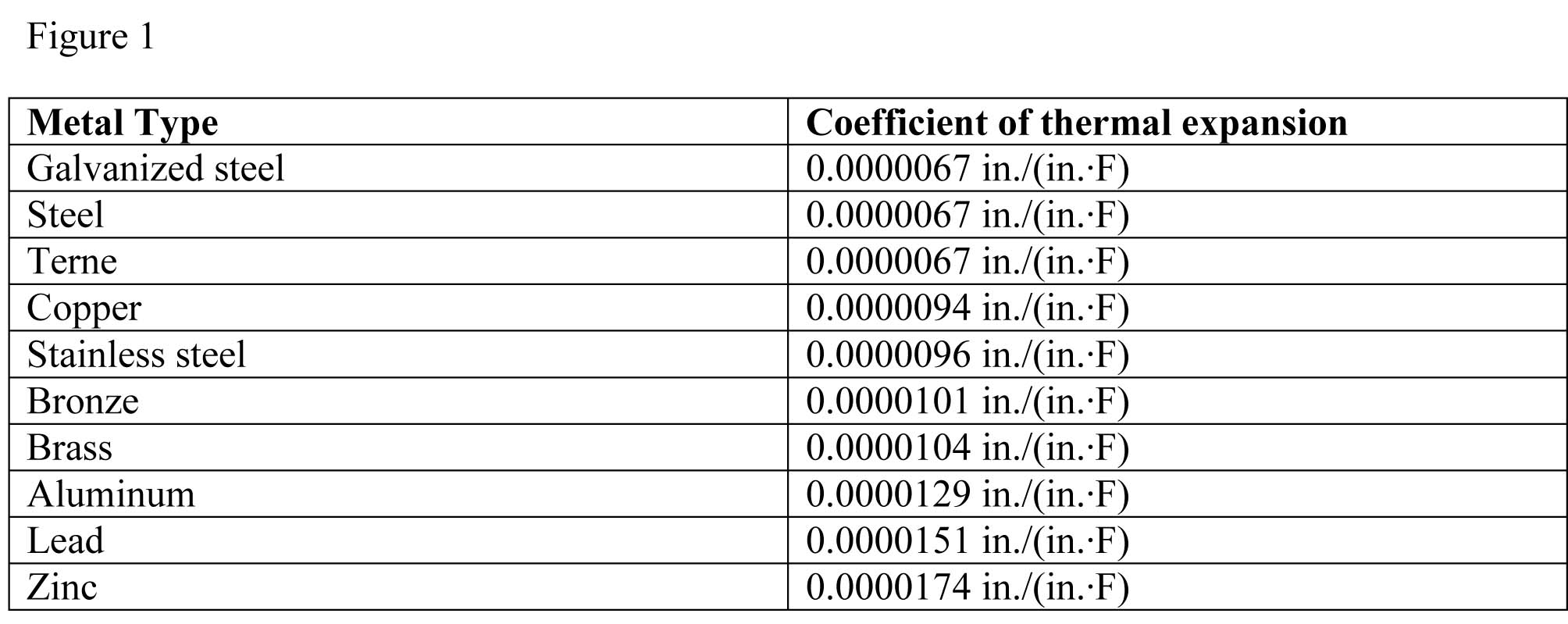
Image courtesy YMCA
Examples
Stresses produced when thermal movement is restrained can be significant. To appreciate the significance of the forces involved, it is helpful to go through an example calculation, step by step.
Example 1
The formula used to calculate a roof panel’s change in length over a temperature swing should be considered as the following equation:
ΔL = a x L x ΔT
In this equation, ‘ΔL’ is the net length change, ‘a’ is the coefficient of linear expansion, ‘L’ is the panel length, and ‘ΔT’ is the expected temperature change.
For a hypothetical scenario, a 12-m (40-ft) panel is formed from a 609-mm (24-in.) wide sheet of 24-gauge steel. The panel is expected to experience service temperatures from –18 to 120 C (0 to 160 F). The linear expansion coefficient for steel (a) is 0.0000067 in./(in.∙F) (or, 0.000012 m/[m∙C]). The net change in length for an unrestrained panel (ΔL) is then calculated as:
ΔL = 0.0000067 in./(in.∙F) x (40 ft x 12 in./ft) x 160 F
= 0.5146 in. (i.e. 13.07 mm)
This value is theoretical. It only works for a panel that is free to expand while supported by a substrate allowing for frictionless movement. If the same panel is prevented from moving by having both ends fixed, it will be under stress from an expansion force (F) proportional to ΔL acting at its fixed ends. The magnitude of F is calculated from the Young’s modulus (E) equation, which is a measure of material stiffness. The value for steel is 200 GPa (29 million psi).
E = stress/strain = (F/A)/( ΔL/L)
In this example, ‘A’ is the panel cross-sectional area. Rearranging the equation, we have:
F = (E x ΔL x A)/L
= (29,000,000 lb/sq.in. x 0.5146 in. x 24 in. x 0.025 in.)/
(40 ft x 12 in./ft)
= 18,654 lb (83 kN)
This value also is theoretical. The calculation assumes the panel is the only element affected by thermal movement. It does not consider thermal movement of the structure restraining the panel at its ends.
The net panel length change and expansion force values in this example reflect idealized conditions not encountered in practice. In real-world applications, the amount of thermal movement is less than the calculated theoretical value, as some of the expansion force is taken up by friction, binding of the clips, flexing of the panel, and rolling of the framing. Field studies have determined this reduction can be as much as 20 per cent below the theoretical value for most systems. Further, from the design perspective, the thermal movement of interest is the panel displacement with relation to the displacement of the substrate, rather than the total panel length change. Thus, calculations need to account for substrate movement in addition to panel movement.


