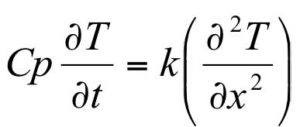Do raked joints affect the fire resistance of concrete masonry?
by Hannah Keelson and Ehab Zalok, P.Eng.

Masonry is employed for a variety of factors such as esthetics, water penetration, and durability. Mortar joints play a significant role in masonry walls as they primarily hold unreinforced masonry walls together and transfer structural/thermal loads. Different forms of mortar joints—concave, flush, raked, beaded, struck, and weathered—can be employed in the construction of masonry walls.
Objective-based National Fire Code of Canada (NFC), as compared to prescriptive codes, attempts to provide a clearer guidance about taking into consideration all functional objectives affecting the fire safety of a structure. These are usually guided by set objectives, and accordingly, met by the designer. In the design of nonloadbearing walls, Canadian Standards Association (CAN/CSA) A371-04, Masonry Construction for Buildings, specifies raked mortar joints for interior-exposed and non-exposed walls. This allows for raked joints to be used once the joints are set just enough to remove excess water. Further, the standard specifies raked joints must be of uniform depth as indicated on drawings. CAN/CSA A371-04 has a “non-mandatory” note that, unless otherwise specified, the joint should be concave for masonry exposed to precipitation. Otherwise, there is no specific mention of mortar joints, where the issue usually arises from an architect’s specifications. The architect may decide to opt for a concave joint just for fire protection reasons, adding to cost, or may allow a struck joint. However, if the joint is not perfectly full, which can happen with a struck joint, the architect will require it to be re-pointed. The lack of any mention of joints in standards or codes had led to the issue. This is probably because until now, there was no test data, so designers default to the more conservative approach.
Architects and clients often prefer the use of raked joints because of their esthetics. However, they have been thought to reduce the fire-resistance properties of concrete masonry. In fact, new research suggests raked and full mortar joints create potential lines of thermal bridging. This would indicate the possibility of having a higher heat transfer around the mortar than the surrounding materials (concrete masonry block), thereby resulting in an overall reduction of the thermal insulation of the wall. In the event of an anticipated fire, the rate of heat transfer could be significantly high, and therefore cause the wall to fail earlier than designed for based on the insulation and integrity criteria per Underwriters Laboratories of Canada (CAN/ULC) S101-14, Standard Methods of Fire Endurance Tests of Building Construction and Materials.
The fire resistance of walls can be determined by performing full-scale tests as per the requirements of objective-based codes. A fire temperature is based on standard fires. Professor Zalok of Carleton University in Ottawa (one of authors of this article) and his research team conducted from 2015 to 2018 full-scale fire tests on nonloadbearing masonry walls constructed with raked and standard concave joints. This was subject to CAN/ULC S101. Experimental fire tests results were used to build a 3D numerical model using finite element software to simulate the process of heat transfer under elevated temperatures.

Images © Hannah Keelson and Ehab Zalok
Building elements and assemblies are normally tested and rated based on their ability to perform intended functions under exposure to standard fires, commonly referred to as “fire-resistance ratings.” This is mostly quantified as the time for the element or assembly to perform its “fire barrier and separation” and/or loadbearing function in the building (This is referenced from Structural Design for Fire Safety by A.H. Buchanan, published in 2002 by John Wiley & Sons.). The experimental work being modelled is part of an ongoing fire-masonry research at Carleton University. A series of walls were constructed and tested as per CAN/ULC S101. Walls were 2.8 m (26 ft) wide and 3.2 m (10.5 ft) tall (seven blocks wide and 16 courses high). Each of the walls was built within a frame of reinforced concrete masonry columns and beams comprising 200 mm (8 in.) normal weight concrete (NWC) hollow block mortared with Type S mortar (Figure 1).
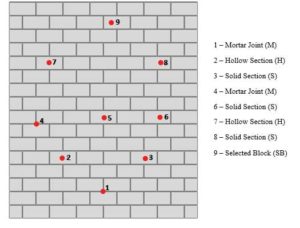
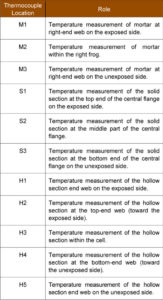
Type S mortar is suitable for general and below-grade uses and, particularly, when high lateral strength is required (Read Masonry Structures Behaviour and Design by R.G. Drysdale and A.A. Hamid, published in 2005 by the Canada Masonry Design Centre (CMDC), for more information.). The strength of the masonry block was 15 MPa (2175 psi). Masonry blocks employed were hollow. Since grout and reinforcement bars were not employed in the construction of the walls, the cells of the block were left hollow. The walls were then subjected to a standard fire temperature curve as prescribed in CAN/ULC S101. The modes of heat transfer on the masonry wall were through convection, radiation, and conduction. Eighteen thermocouples—nine on each side—were employed to measure the temperature of the exposed and unexposed sides of the wall (Figure 2).

Masonry walls are anisotropic (i.e. properties are directionally dependent) in geometry and moisture content. Therefore, three different locations were chosen to place thermocouples. The locations include the mortar joint (M1 to M3), solid section (S1 to S3), and hollow cells (H1 to H5) (Figure 3). At the ninth position, the temperatures at different locations within a block (known as the selected block) was further evaluated. The tested walls were constructed with raked and fully tooled mortar joints (control). Recorded temperatures varied based on these locations. Therefore, these locations and sections were taken into consideration for the numerical study.
A 3D finite element model was developed to simulate the heat transfer process within the wall when subjected to elevated temperatures. The model was first validated against the experimental results from the control wall (concave-jointed walls). Once this was achieved, raked walls were modelled and simulated in a non-linear thermal procedure. Heat analysis involved a pure thermal analysis and, as such, no mechanical behaviour was accounted for.
Where Cp = specific heat capacity (J/kg.K), T = temperature (K), t = time (s), k = thermal conductivity (W/m.K), and
x = thickness of the wall (m).
Simulation procedure
The main components of a finite element model in analyzing a pure heat transfer problem are the element discretization and meshing, material and interaction modules, thermal load, and boundary conditions in addition to the selected solution procedure.
The element discretization and meshing involved creating parts and putting them together in the assembly module (Figure 4). Mesh sizes and types were controlled by geometry, discontinuities, and contact interactions of the assembly. Based on the element type, an eight-node linear interpolation diffusion heat transfer brick (DC3D8) element was used to simulate the heat flow through the component’s assembly for the heat transfer model. The degree of freedom exhibited by using this element is the scalar temperature (nodal temperature [NT11]).
The finite element analysis (FEA) software therefore provides an option to define temperature-dependent properties required in defining properties for heat transfer calculations in solid materials, including:
- density (r);
- specific heat capacity (Cp); and
- thermal conductivity (k).
Based on the thermal load and boundary conditions, the various modes of heat transfer were effectively incorporated into the heat transfer analysis, and defined in the interaction model. The heat source was a uniform net heat flux—![]() (W/m2). The geometry of the masonry wall was divided into exposed surface (hot), unexposed surface (cold), and the side surfaces were considered unexposed as they were insulated.
(W/m2). The geometry of the masonry wall was divided into exposed surface (hot), unexposed surface (cold), and the side surfaces were considered unexposed as they were insulated.
where hc = convection co-efficient; Tf = furnace temperature (K), Ts = surface temperature (K),
![]() = configuration factor,
= configuration factor, ![]() = effective emissivity,
= effective emissivity, ![]() = Stefan-Boltzmann constant (5.67×108 W/m2K4).
= Stefan-Boltzmann constant (5.67×108 W/m2K4).
The estimated heat flux was incorporated as a boundary condition to the modelled assembly through an edited user distributed flux (DFLUX) subroutine (Referenced from L. Peng’s 2010 PhD thesis at Carleton University, Ottawa, on “Performance of Heavy Timber Connections in Fire.”). This is a set of computer programming instructions, which is used for simulation of applying thermal loads on a model assembly. This heat flux can be applied non-uniformly during the heat transfer analysis as a function of element number, integration point of the assembly, position, time, and temperature.
Procedure of the finite element solution
Non-linear numerical simulation was considered due to the non-linearity of the material properties with temperature. To incorporate this into the finite element solution, a pure heat transfer analysis was conducted on the entire assembly. This form of analysis requires primarily inputting an ambient temperature to the entire assembly at the start of the test. A “predefined field” serves as the input for this temperature in the FEA software. A transient heat transfer step including the interaction model with both surface film condition and radiation was then applied. Application of two-boundary conditions for the hot and cold surfaces followed the release of the interaction module based on the results obtained in the previous step. The full Newton method was adopted for the transient heat analysis. This method is an iterative scheme, which can resolve potential non-linearities during the heat transfer analysis. The sources of these non-linearities include the non-linear temperature-dependent properties of the materials and radiation heat flux effects. A nodal temperature-time history at all points in the assembly during the duration of the fire exposure was obtained from this analysis.

Images © H. Pope and Ehab Zalok
Results
The predictions of the finite element model in this research were validated against the outcomes of the full-scale fire experiment described earlier. The evaluation of the finite element model included the comparison between mortar sections during simulations in the model predicting moisture evaporation, when temperatures were within possible range of evaporation (Figure 5a and 5b). Finite element model observations show the solid sections gain more temperature and heat up faster than the other sections (Figure 6).
Concave and raked walls

In both numerical and experimental studies, for both raked and control walls, top block courses recorded highest temperatures compared to bottom courses within the mortar, solid, or hollow sections. This could be attributed to the movement of buoyant hot gases, which rise rapidly to the topmost part of the wall during fire, thereby making the wall hotter at the top than at the bottom, as observed in the experimental study. To achieve this simulation in the numerical model, the application of the DFLUX subroutine file coupled with the effective interaction module ensures this behaviour can be reproduced. This also includes boundary conditions set around the wall. Heat transfer occurs non-linearly, thereby producing higher temperatures at the top of the wall compared to the bottom, as observed in the experimental study.
To predict the thermal behaviour of a masonry block at different sections, a special block was selected and various nodal temperatures were taken for the M, H, and S sections. In the special block, the locations of interest were M3, H5, and S3, as these were on the unexposed side of the wall. H5 recorded highest temperatures right from the start of the analysis. This could be attributed to the air cavities within this section and the rapid transfer of heat by convection and radiation. Additionally, S3 records a higher temperature as compared to M3, as it conducts heat rapidly through the web. Comparatively, the main modes of heat transfer are through convection and radiation. This affirms the higher temperatures recorded by H5. However, at around 90 C (194 F), M3 records a higher temperature than H5 and S3 for both cases. This could be attributed to the moisture content within M3—it contains the highest moisture content, and therefore would require a higher temperature to evaporate the moisture. This process lags on until all the moisture is evaporated, and explains why it takes a relatively lengthy duration while maintaining the same temperature. The results are similar to the experimental study for both walls.

Image © Hannah Keelson and Ehab Zalok
In comparing the average temperature for both walls, the temperatures were closely in line with the recorded temperatures from the experimental work.
Conclusion
Numerical simulations can be used to assess the fire resistance of raked and fully tooled mortar joints in masonry walls as an alternative to full-scale fire-resistance tests. A pure heat transfer analysis procedure in finite element model generally represents the thermal response of the masonry walls in fire conditions. The model’s predictions for the fire resistance of both cases were closely within the temperatures recorded in the experimental study. This significant finding verifies the fire resistance of raked and full mortar joints walls does not depend on the thickness of the mortar, and these two types of wall joints have similar thermal behaviour and fire resistance.
 Hannah Keelson is an assistant project manager at CFT Engineering Inc. She holds a master’s degree in civil and environmental engineering from Carleton University. Keelson’s research focused on simulating the thermal behaviour of non-loadbearing masonry walls that are subjected to elevated temperatures using a numerical modelling. She can be reached at HKeelson@cftengineering.com.
Hannah Keelson is an assistant project manager at CFT Engineering Inc. She holds a master’s degree in civil and environmental engineering from Carleton University. Keelson’s research focused on simulating the thermal behaviour of non-loadbearing masonry walls that are subjected to elevated temperatures using a numerical modelling. She can be reached at HKeelson@cftengineering.com.
Ehab Zalok, P.Eng., is an associate professor at the civil/environmental engineering department at Carleton University. He  holds a PhD in fire safety engineering. His research interests include fire-structure interaction, impact of fires on structures, reinforced concrete, masonry, and steel structures, evaluation of structural aspects of fire safety in buildings, behaviour of fires in enclosures using experimental work and computer modelling, identification of fire hazard in buildings, and developing performance-based fire-structural designs. Zalok is a member of the Society of Fire Protection Engineers (SFPE), Conseil International du Bâtiment (CIB) W14, and a registered Professional Engineer in Ontario. He can be reached at ehab.zalok@carleton.ca.
holds a PhD in fire safety engineering. His research interests include fire-structure interaction, impact of fires on structures, reinforced concrete, masonry, and steel structures, evaluation of structural aspects of fire safety in buildings, behaviour of fires in enclosures using experimental work and computer modelling, identification of fire hazard in buildings, and developing performance-based fire-structural designs. Zalok is a member of the Society of Fire Protection Engineers (SFPE), Conseil International du Bâtiment (CIB) W14, and a registered Professional Engineer in Ontario. He can be reached at ehab.zalok@carleton.ca.